Grade 8 - Claim 1 - Target H

 Back to Results
Back to ResultsClaim 1
Concepts and Procedures
Standards
G-6
Explain a proof of the Pythagorean Theorem and its converse.
G-7
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
G-8
Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.
Clarifications
Tasks associated with this target will ask students to use the Pythagorean Theorem to solve real–world and mathematical problems in two and three dimensions, including problems that ask students to find the distance between...
Range Achievement Level Descriptors
Evidence Required
1
The student solves real–world and mathematical problems of right triangles in two and three dimensions by...
2
The student finds the distance between two points in a coordinate system by applying the Pythagorean...
Item Guidelines

Depth of Knowledge
M-DOK2
Skill/Concept includes the engagement of some mental processing beyond a habitual response. A Level 2 assessment item requires students to make some decisions as to how to approach the problem or activity, whereas Level 1 requires students to demonstrate a...
Allowable Item Types
- Equation/Numeric
- Matching Tables
- Multiple Choice, single correct response
Allowable Stimulus Materials
Two–dimensional representations of triangles, three–dimensional models that contain right triangles, and coordinate systems
Key/Construct Relevant Vocabulary
Pythagorean Theorem, leg, hypotenuse, right triangle, base
Allowable Tools
Calculator
Target-Specific Attributes
The size of the coordinate system must be considered for items that involve the use of coordinate systems.
Accessibility
Item writers should consider the following Language and Visual Element/Design guidelines [1] when developing items. Language Key Considerations: Use simple, clear, and easy-to-understand language needed to assess the construct or aid in the understanding of the...
Development Notes
8.G.B.6 Explaining a proof of the Pythagorean Theorem will be assessed in connection with targets from Claim 3. Some applications of the Pythagorean Theorem will be assessed at deeper levels in Claims 2 and...


Task Models
Task Model 1a

Item Types
Equation/NumericDepth of Knowledge
M-DOK2
Target Evidence Statement
The student solves real–world and mathematical problems of right triangles in two and three dimensions by applying the Pythagorean Theorem and its converse.
Allowable Tools
Calculator
Task Description
Prompt Features: The student is prompted to apply the Pythagorean Theorem to identify an unknown side length of a right triangle. Stimulus Guidelines: Context should be familiar to 13–15 year olds. Item difficulty can be adjusted via...
Stimulus
The student is presented with a situation in two or three dimensions where the Pythagorean Theorem must be used to determine the missing sides of the right triangle.
Example 1
Example Stem 1: A right triangle is shown.
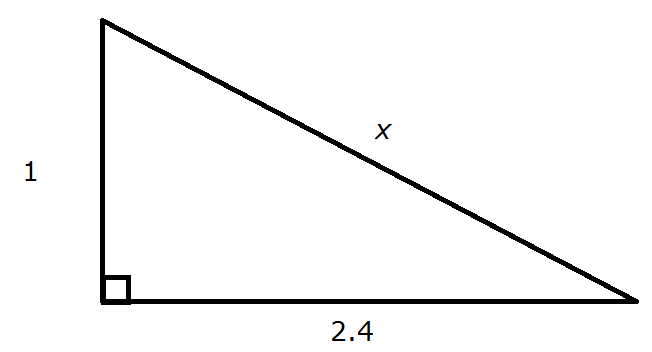
Enter the value of x in the response box.
Rubric: (1 point) Student enters correct value (e.g., 2.6).
Example 2
Example Stem 2: A right square pyramid is shown. The height of the pyramid is 4 units. The distance from the center of the base of the pyramid to vertex D is 3 units, as shown.
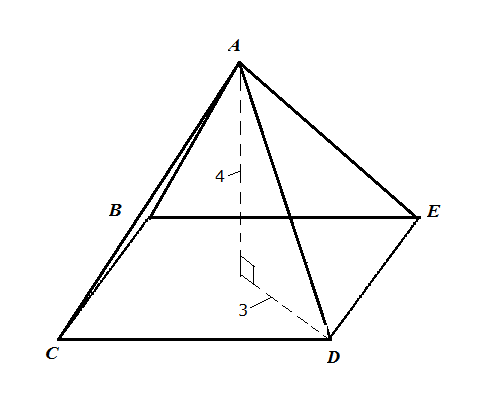
Enter the length of segment AD, in units in the response box.
Rubric: (1 point) Student enters correct value (e.g., 5).
Example 3
Example Stem 3: A 13-foot ladder is leaning on a tree. The bottom of the ladder is on the ground at a distance of 5 feet from the base of the tree. The base of the tree and the ground form a right angle as shown.
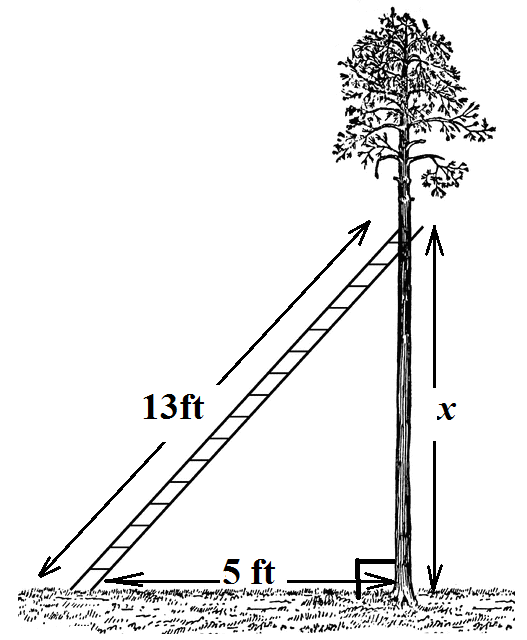
Enter the distance between the ground and the top of the ladder, x, in feet in the response box.
Rubric: (1 point) Student enters correct value (e.g., 12).

