Grade 8 - Claim 1 - Target F

 Back to Results
Back to ResultsClaim 1
Concepts and Procedures
Standards
F-4
Construct a function to model a linear relationship between two quantities. Determine the rate of change and...
F-5
Describe qualitatively the functional relationship between two quantities by analyzing a graph (e.g., where the function...
Clarifications
Tasks for this target will ask students to construct a function to model a linear relationship between two quantities and determine the rate of change or initial value of a linear function from given...
Range Achievement Level Descriptors
Evidence Required
1
The student constructs a function to model a linear relationship between two quantities.
2
The student determines the rate of change and initial value of a function, either from a description of a relationship or from two (x, y) values, including reading the rate of change...
3
The student interprets the rate of change and the initial value of a linear function in terms of the situation it models, its graph, or a table of values.
4
The student qualitatively describes the functional relationship between two quantities by analyzing a graph (e.g., whether the function is increasing or decreasing, or whether the graph is linear or nonlinear).
5
The student draws a graph that exhibits the qualitative features of a function that has been described in writing.
Item Guidelines

Depth of Knowledge
M-DOK1
Recall includes the recall of information such as fact, definition, term, or a simple procedure, as well as performing a simple algorithm or applying a formula. That is, in mathematics a one-step, well-defined, and straight algorithmic procedure should be...
M-DOK2
Skill/Concept includes the engagement of some mental processing beyond a habitual response. A Level 2 assessment item requires students to make some decisions as to how to approach the problem or activity, whereas Level 1 requires students to demonstrate a...
Allowable Item Types
- Equation/Numeric
- Matching Tables
- Multiple Choice, single correct response
- Graphing
Allowable Stimulus Materials
Graphs, equations, tables, written descriptions
Key/Construct Relevant Vocabulary
Function, slope, y–intercept, linear, nonlinear, rate of change, increasing, decreasing, constant, interval, relation
Allowable Tools
Calculator
Target-Specific Attributes
None
Accessibility
Item writers should consider the following Language and Visual Element/Design guidelines [1] when developing items. Language Key Considerations: Use simple, clear, and easy-to-understand language needed to assess the construct or aid in the understanding of the...
Development Notes
Function notation is not required in Grade 8. Items and tasks developed for the Grade 8 Function domain should not use formal function notation [i.e., f(x)]. [1] [1] Items that use function notation may appear...


Task Models
Task Model 1

Item Types
Equation/NumericDepth of Knowledge
M-DOK2Standards
F-4
Target Evidence Statement
The student constructs a function to model a linear relationship between two quantities.
Allowable Tools
Calculator
Task Description
Prompt Features: The student is prompted to construct a linear function given a linear relationship between two quantities. Stimulus Guidelines: Tables should be labeled. Graph scale should contain only integers. Context should be familiar to students 13 to...
Stimulus
The student is presented with a table of input and output values, a graph, or a verbal statement that represents a linear function.
Example 1
Example Stem 1: This table of values represents a linear function.
| x | y |
|---|---|
| 2 | –6 |
| 3 | –6.5 |
| 8 | –9 |
Enter an equation in the form y = mx +b that represents the function.
Rubric: (1 point) Student enters the correct equation (e.g., y = – 0.5x – 5).
Example 2
Example Stem 2: This graph represents a linear function.
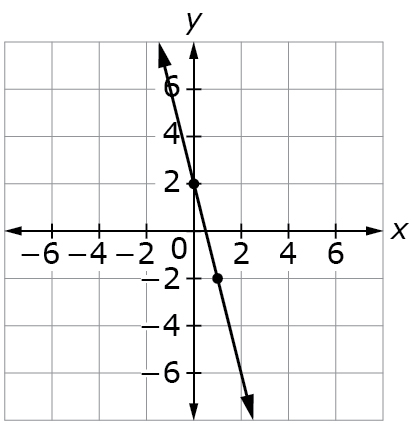
Enter an equation in the form y = mx +b that represents the function.
Rubric: (1 point) Student enters the correct equation (e.g., y = – 4x + 2).
Example 3
Example Stem 3: A swimming pool with 1600 gallons of water is emptied at a constant rate of 300 gallons every 2 hours.
Enter an equation in the form y = mx +b that represents the amount of water y, in gallons, remaining in the pool after x hours.
Rubric: (1 point) Student enters the correct equation (e.g., y = – 150x + 1600).

