Skip to content
Smarter Content Explorer

Grade 8 - Claim 1 - Target E

Back to Results

Mathematics

Target E

Define, evaluate, and compare functions.

Sample Item

Grade 8

Test

Claim 1

Concepts and Procedures

Students can explain and apply mathematical concepts and carry out mathematical procedures with precision and fluency.

Grade

Grade 8

Content Domain

Functions

Standards

F-1F-2F-3
Major

Standards

  • F-1

    Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the...

  • F-2

    Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a linear function represented by a table of values and...

  • F-3

    Interpret the equation y = mx + b as defining a linear function, whose graph is a straight line; give examples of functions that are not linear. For example, the function $A = s^2$ giving...

Clarifications

Tasks associated with this target ask students to relate different representations of functions (equations, graphs, tables, or verbal descriptions). Some tasks for this target will ask students to produce or identify input and output...

Range Achievement Level Descriptors

Evidence Required

  • 1

    The student recognizes that a function is a rule that assigns to each input exactly one output.

  • 2

    The student identifies or produces input and output pairs for given functions.

  • 3

    The student recognizes the same function written in different functional forms (algebraic, graphic, tabular, or verbal).

  • 4

    The student compares properties of two functions, each represented in a different way (algebraic, graphic, tabular, or verbal).

  • 5

    [Retired this Evidence Required statement]

  • 6

    The student recognizes and gives examples of functions that are not linear.

Item Guidelines

Depth of Knowledge

  • M-DOK1

    Recall includes the recall of information such as fact, definition, term, or a simple procedure, as well as performing a simple algorithm or applying a formula. That is, in mathematics a one-step, well-defined, and straight algorithmic procedure should be...

  • M-DOK2

    Skill/Concept includes the engagement of some mental processing beyond a habitual response. A Level 2 assessment item requires students to make some decisions as to how to approach the problem or activity, whereas Level 1 requires students to demonstrate a...

Allowable Item Types

  • Multiple Choice, single correct response
  • Multi-Select, multiple correct response
  • Matching Tables

Allowable Stimulus Materials

equations that define functions, graphical representations of functions, functions represented by tables, written descriptions of functions, sets of ordered pairs

Key/Construct Relevant Vocabulary

function, relation, linear, nonlinear, ordered pairs, coordinate grid, rate of change, y–intercept, x–intercept, slope

Allowable Tools

Calculator

Target-Specific Attributes

None

Accessibility

Item writers should consider the following Language and Visual Element/Design guidelines [1] when developing items. Language Key Considerations: Use simple, clear, and easy-to-understand language needed to assess the construct or aid in the understanding of the...

Development Notes

Function notation is not required in grade 8. Items and tasks developed for the grade 8 Function domain should not use formal function notation [i.e., f(x)]. [1] [1] Items that use function notation may appear...

Task Models

Task Model 1a

  • Item Types

    Multiple Choice, single correct response

  • Depth of Knowledge

    M-DOK1

  • Standards

    F-1

Target Evidence Statement

  • The student recognizes that a function is a rule that assigns to each input exactly one output.

  • Allowable Tools

    Calculator

Task Description

Prompt Features: The student identifies a function as a rule that assigns each input value to exactly one output value. Stimulus Guidelines: Linear equations should be in either y = mx + b where b ≠...

Stimulus

The student is presented with relations that may be functions and are represented as tables, graphs, and equations.

Example 1

Example Stem: Which relation defines y as a function of x?

A. The proportional relationship y = 2.4x.

B. The table showing the age in years, x, and weight in pounds, y, of five dogs.

x y
3 30
4 38
4 21
5 9
6 42

C. The graph of an inequality as shown by the shaded region.

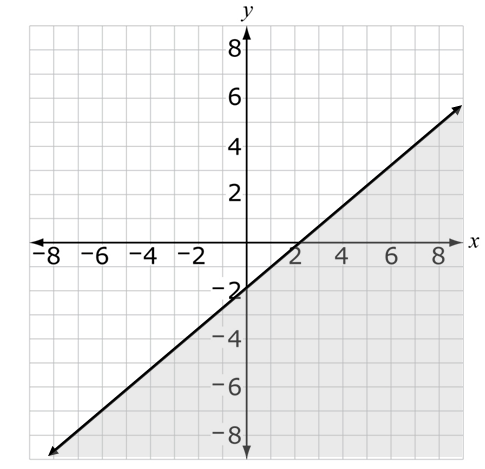
Graph

D. The graph of x2+y2=36x^{2} + y^{2} = 36 as shown.

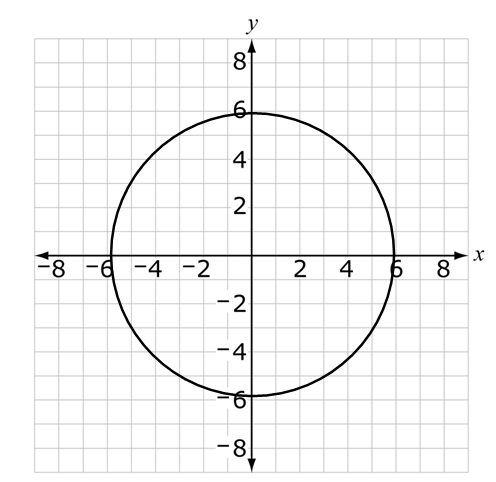
A circle is shown on a coordinate grid with x and y axes ranging from negative 8 to 8. The points where the circle crosses the x and y axis are (6, 0); (0, 6); (negative 6, 0); and (0, negative 6).

Rubric: (1 point) The student selects the relation that is a function (e.g., A).