Skip to content
Smarter Content Explorer

Grade 6 - Claim 2 - Target A

Back to Results

Mathematics

Target A

Apply mathematics to solve well-posed problems in pure mathematics and arising in everyday life, society, and the workplace.

Sample Items

Grade 6Grade 7Grade 8

Tests

Claim 2

Problem Solving

Students can solve a range of complex well-posed problems in pure and applied mathematics, making productive use of knowledge and problem-solving strategies.

Secondary Claim(s)

Items/tasks written primarily to assess Claim 2 will necessarily involve some Claim...

Grades

Grades 6 - 8

Primary Content Domain

Each item/task should be classified as having a primary, or dominant, content...

Secondary Content Domain

While tasks developed to assess Claim 2 will have a primary content...

Clarifications

Problem solving, which of course builds on a foundation of knowledge and procedural proficiency, sits at the core of doing mathematics. Proficiency at problem solving requires students to choose to use concepts and procedures...

  • Assessment Clarifications

    Any given item/task should provide evidence for two or more Claim 2 assessment targets. Each of the following targets should not lead to a separate task: it is in using content from different areas, including work studied in earlier grades,...

  • Target-Specific Assessment Clarification

    Under Claim 2, the problems should be completely formulated, and students should be asked to find a solution path from among their readily available tools.

  • Claim # Sufficient Evidence

    What sufficient evidence looks like for Claim 2 (Problem Solving): "Although items and tasks designed to provide evidence for this claim must primarily assess the student‘s ability to identify the problem and to arrive at an acceptable solution, mathematical problems...

  • Claim # Item / Task Properties

    Properties of items/tasks that assess Claim 2: The assessment of many relatively discrete and/or single-step problems can be accomplished using short constructed-response items, or even computer-enhanced or selected-response items. More extensive constructed-response items can effectively assess multi-stage problem solving and can...

Item Writing and Scoring Guidelines

  • Allowable Response Item Types

    • Drag and Drop
    • Equation/Numeric
    • Fill-In Table
    • Graphing
    • Hot Spot
    • Matching Tables
    • Multi-Select, multiple correct response
    • Multiple Choice, single correct response

  • General Guidelines

    No more than six choices in MS and MA items.

    Short Text – Performance tasks only

  • Scoring Guidelines

    Scoring rules and answer choices will focus on students’ ability to solve problems and/or to apply appropriate strategies to solve problems. For some problems, multiple correct responses and/or strategies are possible. MC will be scored as correct/incorrect (1 point) If MS and...

Range Achievement Level Descriptors

Item Guidelines

Depth of Knowledge

  • M-DOK1

    Recall includes the recall of information such as fact, definition, term, or a simple procedure, as well as performing a simple algorithm or applying a formula. That is, in mathematics a one-step, well-defined, and straight algorithmic procedure should be...

  • M-DOK2

    Skill/Concept includes the engagement of some mental processing beyond a habitual response. A Level 2 assessment item requires students to make some decisions as to how to approach the problem or activity, whereas Level 1 requires students to demonstrate a...

  • M-DOK3

    Strategic Thinking requires reasoning, planning, using evidence, and a higher level of thinking than the previous two levels. In most instances, requiring students to explain their thinking is a Level 3. Activities that require students to make conjectures are also...

Allowable Stimulus Materials

Effort must be made to minimize the reading load in problem situations. Use tables, diagrams with labels, and other strategies to lessen reading load. Use simple subject-verb-object (SVO) sentences; use contexts that are familiar...

Key/Construct Relevant Vocabulary

Refer to the Claim 1 specifications to determine construct-relevant vocabulary associated with specific content standards.

Allowable Tools

Any mathematical tools appropriate to the problem situation and the Claim 1 target(s). Some tools are identified in Standard for Mathematical Practice 5 and others can be found in the language of specific standards....

Target-Specific Attributes

CAT items should take from 2 to 5 minutes to solve; Claim 2 items that are part of a performance task may take 5 to 10 minutes.

Accessibility

Item writers should consider the following Language and Visual Element/Design guidelines [1] when developing items. Language Key Considerations: Use simple, clear, and easy-to-understand language needed to assess the construct or aid in the understanding of the...

Development Notes

Tasks generating evidence for Claim 2 in a given grade will draw upon knowledge and skills articulated in the progression of standards up through that grade, though more complex problem-solving tasks may draw upon...

General Task Model Expectations

General Task Model Expectations for Target 2A: The student is asked to solve a well-posed problem arising in a mathematical context or a context from everyday life, society, or the workplace. Mathematical information from the context...

Task Models

Task Model 1

Task Description

Students use ratios, rates or proportional relationships to solve a problem arising in a real-world context. Dimensions along which to vary the task include a. Using ratios of whole numbers (Grade 6, Example Item a) versus...

Examples

  • Example Item
    2A.1a
    Item Types
    Equation/Numeric, Fill-In Table, Hot Spot
  • Grade
    6
    Targets

    Primary Target 2A (Content Domain RP), Secondary Target 1A (CCSS 6.RP.A), Tertiary Target 2D

Full Statement

Tim made 80 gallons of paint by mixing 48 gallons of green paint with 32 gallons of blue paint. What part of every gallon is from green paint? The picture represents 1 gallon of mixed paint. Click on the picture to show how much of the gallon is from green paint. A cylinder is labeled 1 gallon and divided into 10 equal sections ranging from 0 point 1 0 to 1 point 0 0 in increments of 0 point 1 0.

  • Rubric

    (1 point) The student clicks on the picture so that 0.6 gallon is shaded.

  • Example Item
    2A.1b
    Item Types
    Equation/Numeric, Fill-In Table, Hot Spot
  • Grade
    6
    Targets

    Primary Target 2A (Content Domain RP), Secondary Target 1A (CCSS 6.RP.A), Tertiary Target 2D

Full Statement

It takes Shaun 90 minutes to complete a 15 mile race. The route, with four checkpoints (labeled A, B, C, and D), is shown. The route, with labels Start, checkpoints A through D, and Finish is shown as an irregular shape. Assume Shaun runs at a constant rate during the race. Complete the table to show Shaun's time, in minutes, and distance, in miles, at each checkpoint. Table with 2 rows and 5 columns. Number of minutes: checkpoint A, blank; checkpoint B, 30; checkpoint C, blank; checkpoint D, 75; Finish, 90. Number of miles: checkpoint A, 3; checkpoint B, blank; checkpoint C, 8 point 5; checkpoint D, blank; Finish, 15.

  • Rubric

    (2 points) The student correctly enters all four missing values in the table.
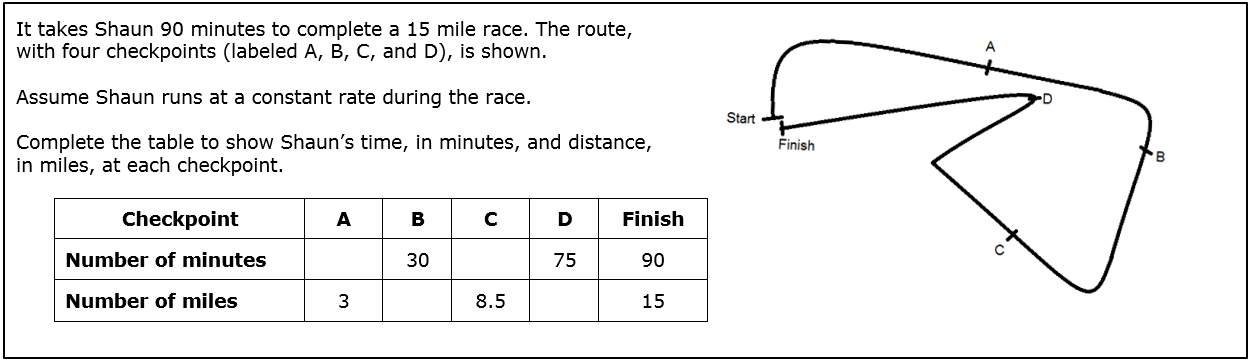
    (1 point) The student correctly determines both minutes (e.g., 18, 51) or both miles (e.g., 5, 12.5) or three out of four values correct.

  • Commentary

    Filling out the different cells in the table requires increasingly sophisticated skills moving from left to right. For students using a unit rate, they must first multiply one-digit whole numbers, then divide a two-digit by a one-digit number resulting in a whole number, then multiply a decimal and a whole number, then divide a two-digit whole number by a one-digit whole number resulting in a decimal. The item could be made easier by changing all entries to require whole-number arithmetic or harder by changing all entries to require decimal number arithmetic. Alternatively, students might notice that the entries in columns A and B are obvious factors of the entries of the columns labeled “Finish” and could easily find their corresponding entries; changing those numbers to less obvious factors would increase the difficulty for students as well.

  • Example Item
    2A.1c
    Item Types
    Equation/Numeric, Fill-In Table, Hot Spot
  • Grade
    6
    Targets

    Primary Target 2A (Content Domain RP), Secondary Target 1A (6.RP.A), Tertiary Standard 2D

Full Statement

Katie and Becca each bought a new book for $50.

  • Katie sold her book to the used bookstore for 25% less than the original price.
  • Becca sold her book to the used bookstore for 40% less than the original price.

Enter how much more money, in dollars, Katie received for her book than Becca received for her book.

  • Rubric

    (1 point) The student enters the correct difference in the response box (e.g., 7.50 or 7 ½).

  • Example Item
    2A.1d
    Item Types
    Equation/Numeric, Fill-In Table, Hot Spot
  • Grade
    7
    Targets

    Primary Target 2A (Content Domain RP), Secondary Target 1A (CCSS 7.RP.A), Tertiary Target 2D

Full Statement

Luke buys a television that is on sale for 25% off the original price. The original price is $120 more than the sale price.

What is the original price of the television?

  • Rubric

    (1 point) The student enters the correct original price in the response box (e.g., 480).

  • Example Item
    2A.1e
    Item Types
    Equation/Numeric, Fill-In Table, Hot Spot
  • Grade
    7
    Targets

    Primary Target 2A (Content Domain RP), Secondary Target 1A (CCSS 7.RP.A), Tertiary Target 2D

Full Statement

Elly poured 110\frac{1}{10} gallon of water into an empty bottle. Now it is 12\frac{1}{2} full. How many cups of water does a full bottle hold?

  • There are 16 cups in one gallon.

Enter the total number of cups that are in the bottle when it is full.

  • Rubric

    (1 point) The student enters the correct number of cups in the response box (e.g., 3 frac15frac{1}{5} or 3.2).

  • Example Item
    2A.1f
    Item Types
    Equation/Numeric, Fill-In Table, Hot Spot
  • Grade
    7
    Targets

    Primary Target 2A (Content Domain EE), Secondary Target 1C (CCSS 7.RP.A), Tertiary Target 2D

Full Statement

Justin’s car can travel 77.5 miles using 3.1 gallons of gas.

At this rate, how far, in miles, can Justin travel using 8.2 gallons of gas?

Enter the distance in the response box.

  • Rubric

    (1 point) The student enters the correct distances in the response boxes (e.g., 205).