Grade 4 - Claim 1 - Target K

 Back to Results
Back to ResultsMathematics
Target K
Geometric measurement: understand concepts of angle and measure angles.
Sample Item
Grade 4Test
Claim 1
Concepts and Procedures
Standards
MD-5
Recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement:
MD-5a
An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the...
MD-5b
An angle that turns through n one-degree angles is said to have an angle measure of n degrees.
MD-6
Measure angles in whole-number degrees using a protractor. Sketch angles of specified measure.
MD-7
Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and...
Clarifications
Tasks for this target will ask students to construct and measure angles using a protractor; to provide multiple ways to decompose a larger angle into two or more smaller angles that have the same...
Range Achievement Level Descriptors
Evidence Required
1
The student relates the concept of an angle to the fraction of a circular arc between two points on a circle.
2
The student uses a protractor to measure angles (composed of one-degree angles) and construct angles to whole-number degrees.
3
The student decomposes an angle into smaller non-overlapping parts and adds the measures of these smaller parts to find the measure of the whole angle.
4
The student solves addition and subtraction problems to find unknown angles on a diagram in real-world and mathematical problems.
Item Guidelines

Depth of Knowledge
M-DOK1
Recall includes the recall of information such as fact, definition, term, or a simple procedure, as well as performing a simple algorithm or applying a formula. That is, in mathematics a one-step, well-defined, and straight algorithmic procedure should be...
M-DOK2
Skill/Concept includes the engagement of some mental processing beyond a habitual response. A Level 2 assessment item requires students to make some decisions as to how to approach the problem or activity, whereas Level 1 requires students to demonstrate a...
Allowable Item Types
- Equation/Numeric
- Drag and Drop
- Graphing
Allowable Stimulus Materials
graphics of angles, turns, and rotations; protractors
Key/Construct Relevant Vocabulary
protractor, angle, ray, intersect, one-degree angle, vertex, ray
Allowable Tools
protractor
Target-Specific Attributes
Benchmark angles are 30°, 45°, 60°, 90°, 180°
Accessibility
Item writers should consider the following Language and Visual Element/Design guidelines [1] when developing items. Language Key Considerations: Use simple, clear, and easy-to-understand language needed to assess the construct or aid in the understanding of the...
Development Notes
Representing the addition or subtraction of angle measures with an equation will be assessed in Claim 4.
Identifying angles of specified measures will be assessed at Claim 2.


Task Models
Task Model 1

Item Types
Equation/NumericDepth of Knowledge
M-DOK2Standards
MD-5
Target Evidence Statement
The student relates the concept of an angle to the fraction of a circular arc between two points on a circle.
Allowable Tools
None
Task Description
Prompt Features: The student is prompted to write the measure of an angle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points...
Stimulus
The student is presented with an angle superimposed on a circle with its vertex at the center of the circle and the fraction of a circular arc that it represents.
Example 1
Example Stem: The vertex of ∠PNR is at the center of the circle. The circular arc between Point P and Point R is of the circle.
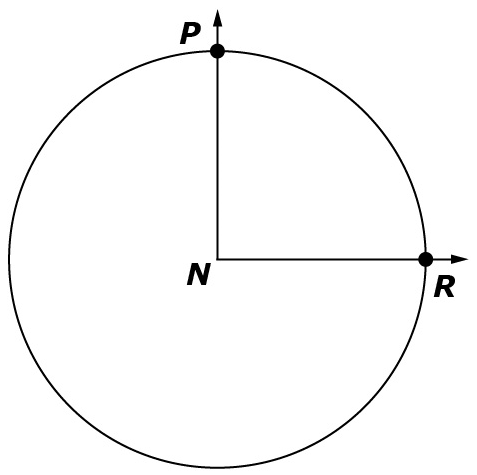
Enter the measure, in degrees, of ∠PNR in the response box.
Rubric: The student enters the correct number of degrees (e.g., 90).

